Tropical geometry is
a fairly recent research field in mathematics named in honour of
its initiator, the Brazilian mathematician and computer scientist
Imre Simon. It is a piecewise linear version of algebraic geometry.
The complicated shapes of algebraic geometry are
replaced by polyhedra, objects with flat sides. The theory often
serves to translate difficult problems in algebraic geometry into
much simpler problems in combinatorics.
The most important applications of tropical geometry in
mathematics so far have been in the enumerative
geometry of curves. This is a classical subject of
algebraic geometry, studied at least since the 19th century. In
recent years it was revolutionized by the input coming from
theoretical physics, in particular from string theory.
One would like to know, for example, how many algebraic curves
satisfy certain suitable conditions; say, how many curves of degree
d in the plane have a given number of singularities (self
intersections) passing through a certain number of general points.
For instance, what is the number of cubics (curves of degree 3) in
the complex plane with one singularity passing through 8 general
points? It is known that this number equals 12. It was proved by
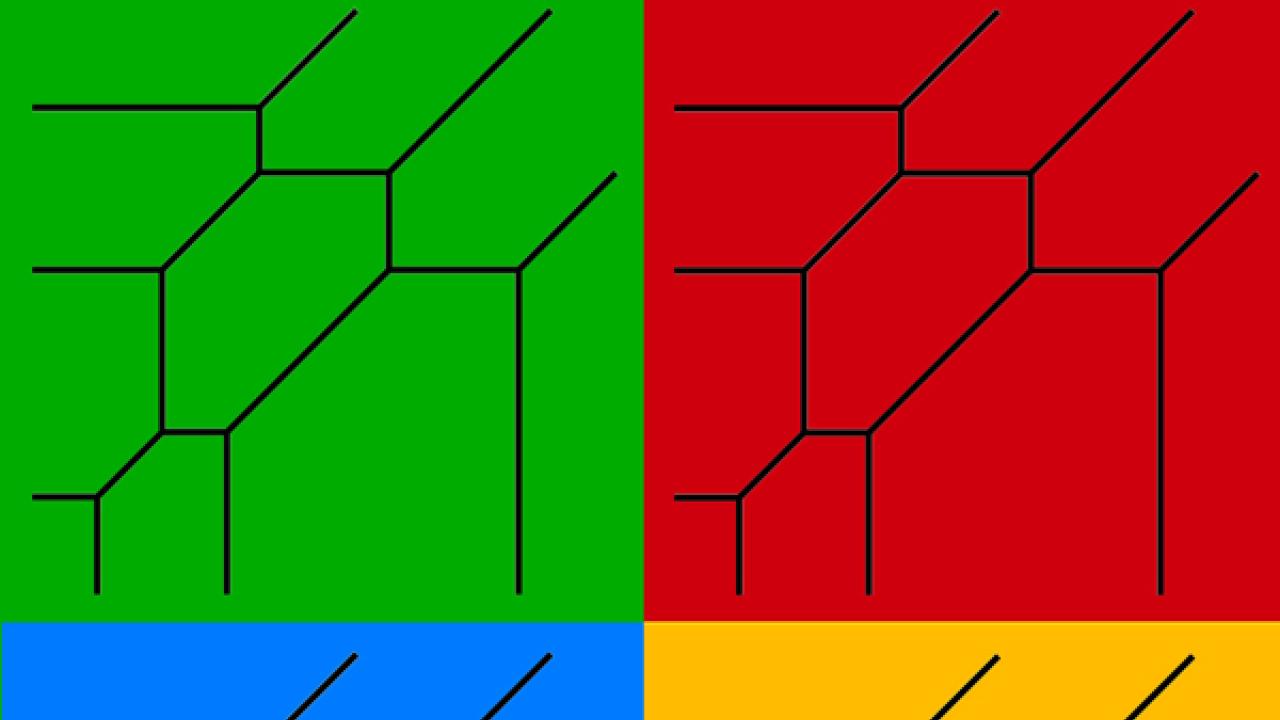
Mikhalkin that the number of such algebraic curves is equal to the
corresponding number of tropical curves, which are just piecewise
linearly embedded graphs in the plane and hence much easier to
understand.
ICTP mathematician Lothar Göttsche has introduced refined
enumerative invariants of curves giving finer invariants than just
the numbers of curves, first in algebraic geometry and then in
tropical geometry. He was asked to give one of this semester's Bernoulli lectures
at the Ecole Polytechnique Federale de Lausanne's (EPFL) Bernoulli
Center in Lausanne, Switzerland, on May 15, on this topic.
The Bernoulli Center is one of the primary research meeting places
in mathematics in Europe. Their thematic programs consist of a six
month period of concentrated activity in a specific area of current
research interest in the mathematical sciences. The activities
during each of these thematic semesters include three special
Bernoulli lectures given by experts in the field. The current
semester's thematic program is on "Tropical geometry in its complex
and symplectic aspects", organized by Ilia Itenberg and Grigory
Mikhalkin.
Gottsche has previously been invited to give two-week lecture
courses on this material at IMPA, the top mathematics research
institute in Brazil, from 14 to 24 2013, and at the graduate school on new aspects on
singularity theory at ICMAT, Madrid, Spain, from 16 to
27 September 2013.